08:45
[익명]
고1 공통수학2 / 파푸스정리 이미지 속 문제를 파푸스 정리를 이용한 풀이와 일반적인 풀이로 나눠서
이미지 속 문제를 파푸스 정리를 이용한 풀이와 일반적인 풀이로 나눠서 각각 해설 부탁드립니다!
사실 이 문제는 거리 구하는 공식을 적용하여, 2차함수의 최소 문제로 생각해도 크게 복잡하지는 않습니다.
하지만, 파푸스정리를 이용하면 매우 간편해집니다.
1. 거리구하는 공식 적용
AP^2 + BP^2 = {(p-1)^2 + 5^2} + {(p+5)^2 + 3^2} = p^2 -2p + 26 + p^2 + 10p + 34
= 2(p^2 +4p + 4) -8 + 60 = 2(p+2)^2 + 52
p = -2일 때, 최소이고 그 최솟값은 52.
2. 파푸스정리 이용
그림에서, M의 좌표는 (-2,4)
AP^2 + AP^2 = 2(PM^2 + AM^2) = 2( PM^2 + (1-(-2))^2 + (5-4)^2 ) = 2( PM^2 + 3^2 + 1^2 )
= 2(PM^2 + 10)
AP^2 + AP^2 은 PM이 최소일 때, 최소. PM은 x축에 수직일 때 최소이므로, 그 최솟값은 4.
구하는 최솟값은
2(PM^2 + 10) = 2×(4^2 + 10) = 2×26 = 52
회원가입 혹은 광고 [X]를 누르면 내용이 보입니다
-
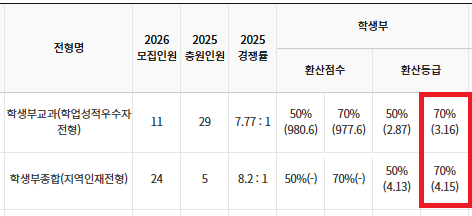
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -

아이폰 16, 16프로 케이스 호환 가능한가요? 16을 쓰고 있는데 일반형은 케이스가 많이 없고 프로형은 많아서
2025.12.01 -

임영웅 11월 브랜드평판 순위 알고싶어요 임영웅 11월 브랜드평판에서 스타부문에서의 임영웅 순위 알고싶어요
2025.11.30 -

전주 고등학교 다자녀 제가 2027학년도 고등학교 입학생인데요 지망하는 학교가 전주 한일고인데 1. 다자녀
2025.11.30 -
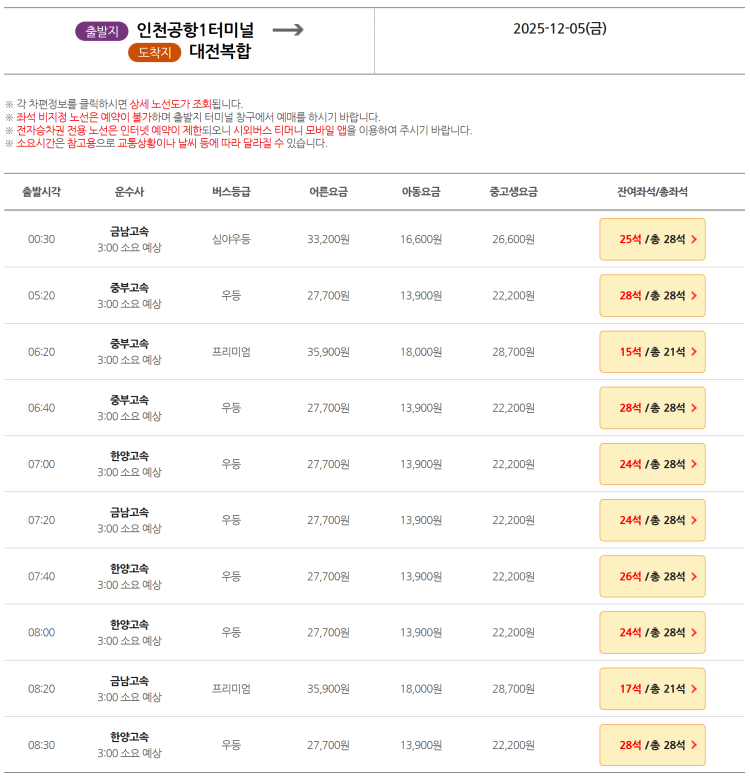
고속버스 예매 인천공항에서 대전으로 가는 버스를 이용하려하는데 버스 노선이 인천공항 2터미널에서 출발해
2025.11.30 -

어떤 야구선수 싸인일까요? 제가 옛날에 롯데 자이언츠 선수한테 싸인받은 싸인볼을 오늘 찾았네요. 어떤
2025.11.29
